Теория вероятности – это раздел математики, связанный с анализом случайных явлений. Исход случайного события нельзя определить до его возникновения, но это может быть любой из нескольких возможных исходов. Фактический результат считается случайным в теории вероятности www.evkova.org/teoriya-veroyatnosti
В обычном разговоре вероятность имеет несколько значений. Два из них особенно важны для развития и приложений математической теории вероятностей. Один из них — это интерпретация вероятностей как относительные частоты, для которых простые игры с монетами, картами, игральными костями и колесами рулетки являются примерами.
Отличительная черта азартных игр состоит в том, что исход данного испытания нельзя предсказать с уверенностью, хотя общие результаты большого числа испытаний обнаруживают некоторую закономерность.
Например, утверждение о том, что вероятность «орла» при подбрасывании монеты равна половине, согласно интерпретации относительной частоты, означает, что при большом количестве подбрасываний относительная частота, с которой на самом деле выпадает «орел», будет примерно равной единице. -половину, хотя и не подразумевает относительно результата любого броска. Есть много подобных примеров с участием групп людей, молекул газа, генов и так далее.
Актуарные утверждения об ожидаемой продолжительности жизни для людей определенного возраста описывают коллективный опыт большого числа людей, но не претендуют на то, чтобы сказать, что произойдет с каким-либо конкретным человеком. Точно так же прогнозы о вероятности возникновения генетического заболевания у ребенка, родители которого имеют известный генетический состав, являются утверждениями об относительной частоте встречаемости в большом количестве случаев, но не являются прогнозами относительно конкретного человека.
Теория вероятностей и математические концепции
Математические концепции теории вероятностей, проиллюстрированных некоторыми приложениями, которые стимулировали их развитие. Для более полного исторического анализа см. Вероятность и статистику .
Поскольку приложения неизбежно включают упрощающие предположения, которые фокусируются на одних особенностях проблемы за счет других, выгодно начинать с размышлений о простых экспериментах, таких как подбрасывание монеты или бросание кости, а затем посмотреть, как эти очевидно несерьезные исследования соотносятся с важными научными вопросами.
Эксперименты, пространство выборки, события и равновероятные вероятности
Приложения простых вероятностных экспериментов
Фундаментальный компонент теории вероятностей — это эксперимент, который можно повторить, по крайней мере, гипотетически, в практически идентичных условиях и который может привести к разным результатам в разных испытаниях. Множество всех возможных исходов эксперимента, называется «выборочное пространство».
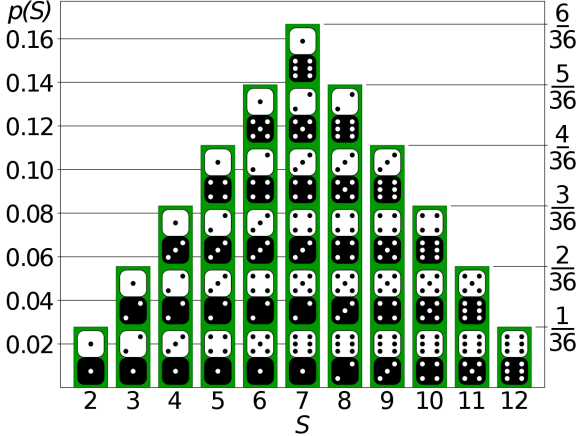
Эксперимент по подбрасыванию монеты один раз приводит пространство выборки с двумя возможными исходами: «орел» и «решка». Подбрасывание двух имеет пространство выборки с 36 возможными исходами, каждый из которых может быть идентифицирован с упорядоченной парой ( i , j ), где i и j принимают одно из значений 1, 2, 3, 4, 5, 6 и обозначают грани показаны на отдельных кубиках. Важно думать о кубиках как о идентифицируемых (скажем, по разнице в цвете), чтобы результат (1, 2) отличался от (2, 1).
«Событие» — это четко определенное подмножество выборочного пространства. Например, событие «сумма лиц, показанных на двух кубиках, равна шести», состоит из пяти исходов (1, 5), (2, 4), (3, 3), (4, 2) и (5, 1) .
Немного сложнее определить вероятность «не более одной головы». В дополнение к единственному случаю, когда голова не возникает, есть n случаев, когда выпадает ровно одна голова, потому что она может произойти при первом, втором,… или n- м броске. Следовательно, существует n + 1 случаев, благоприятных для получения не более одной головы, и желаемая вероятность равна ( n + 1) / 2 n .
Фундаментальные примеры теории вероятностей
Этот последний пример иллюстрирует фундаментальный принцип: если событие, вероятность которого ищется, можно представить как объединение нескольких других событий, которые не имеют общих исходов («максимум одна голова» — это объединение «без голов» и «ровно одна голова»), тогда вероятность объединения — это сумма вероятностей отдельных событий составляя союз. Чтобы описать эту ситуацию символически, пусть S обозначает пространство отсчетов.
Для двух событий A и B пересечение A и B представляет собой набор всех экспериментальных результатов, принадлежащих как A, так и B, и обозначается A ∩ B ; объединение A и B это совокупность всех экспериментальных результатов , относящихся к A или B (или оба) и обозначается A ∪ B . Невозможное событие, т. е. событие, не содержащее результатов, обозначается символом Ø. Вероятность события A записывается P ( A ). Принцип сложения вероятностей состоит в том, что если A 1 , A 2 ,…, A n — события с A i ∩ A j = Ø для всех пар i ≠ j , то [Уравнение.]
Уравнение (1) согласуется с относительной частотной интерпретацией вероятностей; поскольку, если A i ∩ A j = Ø для всех i ≠ j , относительная частота, с которой встречается хотя бы один из A i, равна сумме относительных частот, с которыми встречается отдельный A i .
Уравнение (1) является фундаментальным для всего последующего. В самом деле, в
современной аксиоматической теории вероятности, которая избегает определения вероятности в терминах «равновероятных исходов» как безнадежно замкнутого круга, расширенная форма уравнения (1) играет основную роль.
Полиномиальная вероятность
Основная проблема, впервые решенная Якобом Бернулли, состоит в том, чтобы найти вероятность получить ровно i красных шаров в эксперименте по случайному вытягиванию n раз с заменой из урны, содержащей b черных и r красных шаров. Случайное вытягивание означает, что при одной розыгрыше каждый из r + b шаров с одинаковой вероятностью будет вытащен, и, поскольку каждый шар заменяется перед следующим розыгрышем, имеется ( r + b ) × ⋯ × ( r + б ) = ( г + б ) возможные результаты эксперимента. Из этих возможных исходов число, которое благоприятно для получения i красных шаров и n — i черных шаров в любом конкретном порядке, равно [Уравнение.]
Количество возможных порядков, в которых из урны могут быть извлечены i красных шаров и n — i черных шаров, является биномиальным коэффициентом [Уравнение.] где к ! = k × ( k — 1) × ⋯ × 2 × 1 для натуральных чисел k и 0! = 1. Следовательно, рассматриваемая вероятность, равная количеству благоприятных исходов, деленному на количество возможных исходов, задается биномиальным распределением.
Приложения условной вероятности
Применение закона полной вероятности к проблеме, первоначально поставленной Христианом Гюйгенсом, состоит в том, чтобы найти вероятность «разорение игрока ». Предположим, у двух игроков, которых часто называют Питером и Полом, изначально есть x и m — x долларов соответственно. Из урны вынимается шар, красный с вероятностью p и черный с вероятностью q = 1 — p . Если выпал красный шар, Пол должен заплатить Питеру один доллар, а Петр должен заплатить Полу один доллар, если выпавший шар черный. Мяч заменяется, и игра продолжается до тех пор, пока один из игроков не разорится. Определить вероятность гибели Петра прямым анализом всех возможных случаев довольно сложно .
Но пусть Q ( x ) обозначает эту вероятность как функцию начального состояния Петра x и обратите внимание, что после одного розыгрыша структура остальной игры в точности такая же, как и до первого розыгрыша, за исключением того, что состояние Петра теперь равно x + 1 или x — 1 в зависимости от результатов первого розыгрыша. рисовать. Закон полной вероятности с A = {красный шар при первом розыгрыше} и A c = {черный шар при первом розыгрыше} показывает, что [Уравнение.]
Это уравнение выполняется для x = 2, 3,…, m — 2. Оно также выполняется для x = 1 и m — 1, если добавить граничные условия Q (0) = 1 и Q ( m ) = 0, которые говорят, что если у Питера изначально 0 долларов, его вероятность разорения равна 1, а если у него все m долларов, он обязательно выиграет.






